|
How to Design Small Decision Making Groups |
|
| Introduction
Teamwork and group decision
making are hot buzz words. Giant corporations
spend millions annually teaching employees how to work in groups and hold
effective meetings. Yet, anyone who has attended a decision making
meeting probably feels that a camel is indeed a horse designed by a
committee. When decision making teams work, they work very well
and when they don't they consume inordinate amounts of time only to yield weak
results. Simple applications of probability and
statistics can shed light on how to stack the odds in favor of success.
This
discussion will focus on decision making groups working with partial
information where there is a definite difference between selecting a
good and bad alternative. For
example, this could be a decision about how many toys to produce for the
Christmas market. There is only partial information since actual customer
behavior cannot be known until well after the decision is
implemented. Making the wrong number of toys can result in a
substantial loss of profit.
Such groups have two key problems. The first is management
of
communication. The second is decision making accuracy.
Generally having more people in a group increases the likelihood that
someone will propose the correct decision. However, more people means
more opinions and ideas that have to be communicated and discussed. This
makes management of the communication process more difficult and can end
up reducing group effectiveness. The best ideas may never even be heard.
Management
of Communication
The difficulty of managing communication is
roughly proportional to the number of possible social interactions.
With two people there is nothing to manage since there is only one
possible social interaction. With three people there are three
possible two-person interactions and one three way interaction for a
total of four. With a four person group there are six possible two
way, four possible three-way, and one possible four way interactions
for a total of eleven. |
|
Rules for Optimizing Small
Groups
- Group members must have the basic
knowledge and ability to identify and evaluate
alternatives. Not everyone needs to be an expert but
everyone must be able to ask
intelligent questions.
- Each member must be granted equal status or standing
within the group. A single member may be the only one
to have the correct solution. Equal status improves the
chances that this solution will be expressed.
- Each member must be allowed to fully explain and
argue
for his or her proposed solutions. This is the only
way a single individual with the correct solution can
convince the group.
- Criticisms of options should be made only after all
options have been listed. This helps insure that
all options are identified.
- For major decisions, discussion should proceed until
there is unanimous agreement that a workable solution has
been reached. Requiring a unanimous agreement forces a
greater amount of discussion and gives a single individual
with the correct solution the opportunity to convince
others. Unanimous agreement can involve compromise. It
means that all the members have agreed to a workable
solution although it may not be their personal favorite.
- For minor decisions, the majority rules. This
speeds up group activities without a major loss of
effectiveness.
- Groups should have an odd number of members. This
prevents ties and improves the odds of making a correct
decision when using majority rules.
- The optimum group size is about 5 members. Groups
should be expanded beyond this size only when there is
good reason. For instance, effective implementation may
require buy-in by more than 5 major stakeholders.
|
|
|
| The total number of
possible social interactions for any sized group is simply the sum
of all possible combinations taken two at a time or higher. These are calculated
for 2-person interactions using the
following Formula:
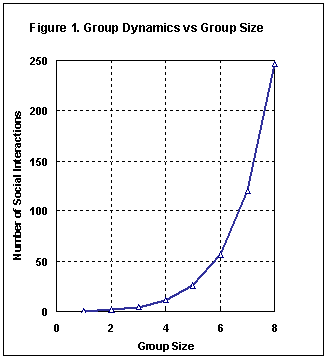
As can be seen by figure 1, the number of
possible social interactions begins to explode in groups with more
than 5 people. Large groups require skillful leaders and formal
structure in order to function effectively. Formal structure, such
as parliamentary procedure, works by deliberately stifling many of
the possible social interactions. Unfortunately, this can also
stifle creativity and insures that decisions will be dominated by
the most politically skillful individuals even when they don't have
the best ideas. |
|
 |
|
|
Best Possible Decision Making Accuracy Probability
can also be used to evaluate decision making accuracy. This can get
complicated so we'll make some simplifying assumptions as follows:
- There is
partial information available on all possible
alternatives. Obviously, if there's no information available then
decision accuracy is random. If complete information is available then
the decision accuracy should depend only on having enough time and expertise
to evaluate the information.
- All alternatives can be clearly categorized as
good or bad. Those categorized as good are clearly superior to
those categorized as bad. Selecting a good alternative is a good
decision by definition. There can be no ties. A decision is either
good or bad.
- The probability of successfully identifying a
superior alternative is not influenced by the number of alternatives.
If bad alternatives greatly outnumber good ones then it does not make
the good ones harder to identify. In real life many bad alternatives
can be quickly eliminated.
- Each group member has the same probability of
successfully identifying a good alternative. A decision
making group should contain qualified people who have the ability to
discuss and analyze the alternatives. When only partial information is
available there typically are no experts with the special ability to
consistently guess the right answer. If such an expert existed then there would be no accuracy advantage in using a group.
|
|
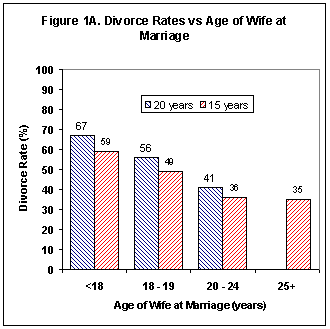
Divorce statistics for
first marriages provide information on the average probability of picking a
good alternative in an important decision using partial information. Failure to pick
a good alternative can be defined
as divorce. Overall, after 20 years 50% of all first
marriages have ended in divorce. Based on
the divorce statistic, it looks like 50% would be a good
number for the average decision making accuracy of typical individuals. However, closer examination
indicates that 50% is a low estimate. Women who marry when
they are less than 18 years old have a 67% chance of ending their first
marriage within 20 years. On average, members of this group have not fully
developed their ability to identify and evaluate alternatives. Their
higher divorce rate skews the average results for all
marriages to the low side.
Women between 20 to 24 years of age, on the other
hand have a 41% chance of divorce within 20 years. This rate appears to
remain approximately stable for women who marry at 25 years of age or older
(see Figure 1A). Based on this information 60% accuracy looks
like a better rule of thumb for adult decision makers who are using partial
information.
|
|
|
Adoption of the 60% average
accuracy rule of thumb is not based on a mathematical proof but is
reasonable. In many cases a 50% average accuracy could be achieved by coin
tossing. It's unlikely for human decision making to be worse on average than 50%
accuracy unless fraud or deception is involved. 60% accuracy seems more
reasonable without being overly optimistic about humankind's abilities. Assuming an
average decision making accuracy of 60% allows us to calculate the
probability that no one in a group will identify a good alternative.
Obviously if this were true then the group could not possibly make a good
decision. The probability of no one in the group identifying a good
alternative is found as follows:
- P0 = (0.4)n
- Where
n = the number of people in the group.
The best possible decision
making accuracy of the group would be Pg = 1 - P0 .
|
|
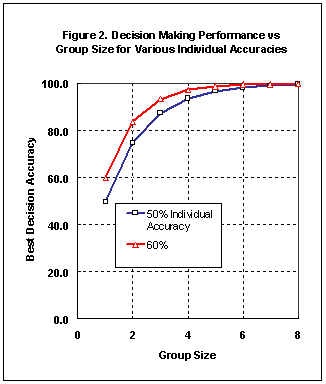
Figure 2 shows a graph of the best possible decision making accuracy vs
group size. To achieve this level requires that the decision be made unanimously following an
extended discussion. The Rules for Optimizing Small Groups shown at the top of the
page must be followed to achieve this performance. These rules are designed
to insure that all options are identified and that they are fully discussed. If the group is composed of qualified individuals with
the basic knowledge to make the decision and they behave in a rational
manner, a single enlightened group member should be able to persuade the
group to select the right alternative. On this basis the only way the group
would fail is if no one in the group selects a good alternative.
Majority Rules Decision Accuracy
There is a tendency in groups to make decisions by voting,
in which the majority rules. While this speeds the decision making process
it reduces the accuracy and should be used only for minor decisions.
To study this situation we resort to finding areas under
the binomial distribution using the following relationship:
| n |
|
|
|
|
| S |
( |
n! |
) |
(qn-x)px |
| x!(n
- x)! |
| x=m |
|
|
|
|
- where:
- n = number of group members
- m = the minimum size for a majority
- p = the probability of being right or .6
- q = the probability of being wrong or .4
- note: q = (1-p )
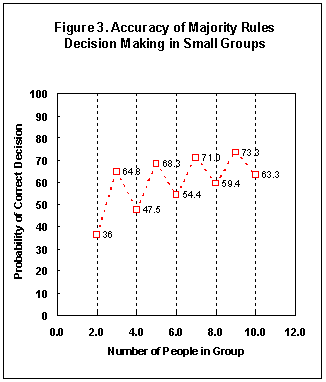
Figure 3 displays the results of majority rules decision
making for various sized groups. Note the odd looking saw tooth appearance
which gives even numbered groups a lower probability of making the correct
decision. The explanation is that these groups can have a tie. For example,
a group of four will only have a majority 75% of the time. The other 25% of
the time will be a tie vote which obviously does not result in a correct decision. Odd
numbered groups will have a majority on every vote. Yes, even number groups
can often resolve tie votes but it costs more time and effort to do
it.
Conclusions:
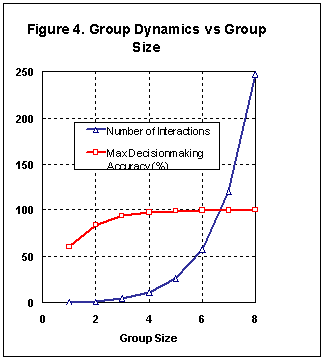
Figure 4. shows that a group size of five is optimum. Five
takes advantage of the desirability of odd numbers
for majority rules decisions. For the unanimous decision making style a group of five will have a 99% accuracy
assuming 60%
individual accuracies and that a single person with the right answer can
convince the others. Even with only 50% individual accuracies the group
accuracy will average 96.9%. Adding additional members will not greatly
improve accuracy. However, additional members will significantly increase
group management problems since the number of possible social
interactions increases rapidly.
The data presented does not mean that every group has to
contain exactly five members. There are other factors to consider such as
the implementation of decisions. This often requires buy-in by the
stakeholders. Placing stakeholders in the group can speed implementation. However, important decision making groups should not be
expanded unless there is an overriding reason to do so.
|
|
|
|
|
 |
|
References
1. Matthew D. Bramlett, Ph.D., and William D. Mosher,
Ph.D., Division of Vital Statistics, "First Marriage Dissolution,
Divorce, and Remarriage: United States", Advance Data Number 323 +May
31, 2001Department of Health and Human Services
< Return to Contents
|
|
|