|
Discrete Distribution Dice Game Problem |
| A dice game pays a player $5
for rolling a 3 or 5with a single die. The player must pay $2 for rolling
anything else. What is the mean and standard deviation of the distribution.
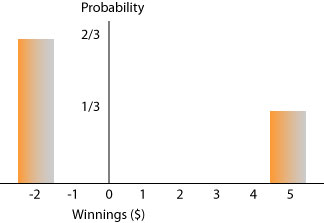
Draw the distribution. * Solution: |
| probability of rolling a 3 or 5 = 1/6 +
1/6 |
 |
|
= 1/3 |
| |
| prob. of rolling 1, 2, 4, 6 = 1/6 + 1/6 +
1/6 + 1/6 |
|
= 2/3 |
| |
| mean = Σ xi pi |
|
= ( - 2 ) 2/3 + ( 5 ) 1/3 |
|
|
| |
| variance = [( -2 -1/3 )^2 ]
∙ 2/3 + [( 5 -1/3 )^2 ] ∙
1/3 |
|
= 10.89 |
|
| standard deviation = ( 10.89)^0.5 |
|
|
standard deviation = 3.30 |
|
|
| |
|
| * The numbers in this
problem were taken from Prepare for the AP Exam Guide for Yates, Moore, and
Starnes's Practice of Statistics, #30, Exam 4, 2003 |
